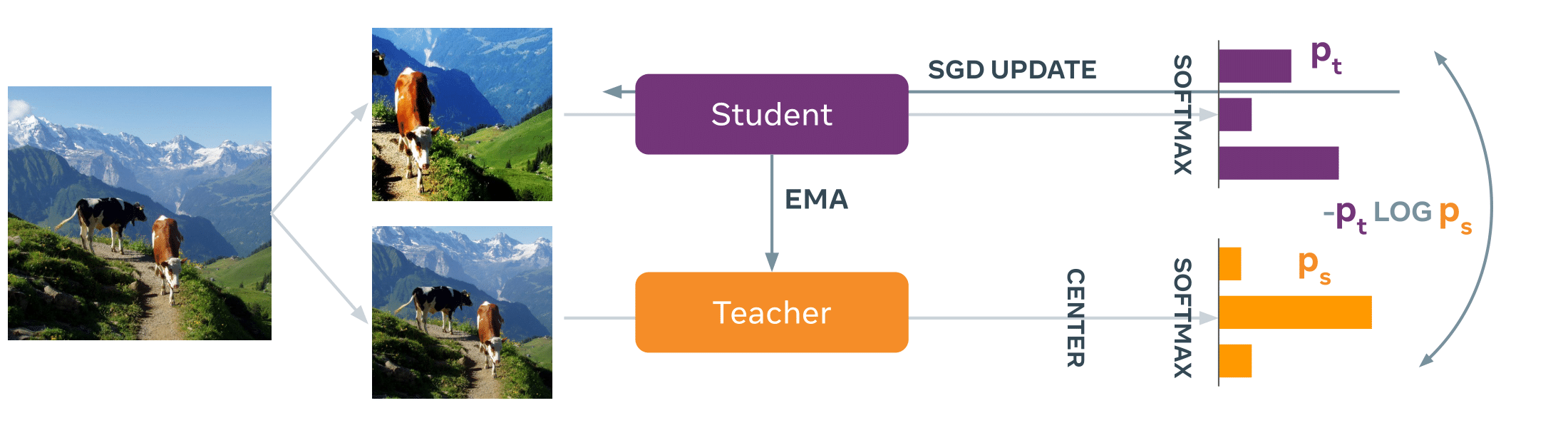
The method is made of:
- A neural network trained with self-supervision that extracts features from images
- An embedding process that shifts the features into a well-specified region of the latent space
- A decoding step that happens in the same latent space
TL;DR (Summary)
Context - Robust watermarking and data hiding:
- Subject to trade-offs: imperceptibility, payload, robustness
- Traditional watermarking algorithms require expert knowledge of the field and hand-crafted implementations for each transformations one wishes to be robust against.
- State of the art deep watermarking architectures require heavy training, lack flexibility w.r.t. parameters of the trade-offs and do not provide guarantees on detection or decodings.
General idea:
- Use intrinsic robustness of features created by self-supervised training and encode information in the resulting latent spaces
Summary of our contributions:
- Encode both marks or binary messages in the latent space of any pre-trained network
- Leverage data augmentation at marking time
- Experimental evidence that self-supervision gives excellent embedding spaces
Poster
Video
Backbone and feature normalization
Self-Supervised Learning with DINO
We use DINO as our backbone, for its good performance in KNN evaluation. Please refer to the DINO paper for more details.
PCA Whitening
Features output by the neural network are not well distributed:
For instance, 0-bit watermarking needs to push features in a hypercone of the latent space. If this hypercone isn’t attainable by the neural network output distribution, the algorithm won’t be able to embed marks.
Therefore, we apply transformation for the features to have zero mean and identity covariance:
- Eigendecomposition of the covariance matrix: \(\Sigma = U\Lambda U^T\)
- Linear transformation: \(x = \Lambda^{-1/2}U^T(x - \bar{\mu})\)

Embedding process
The goal of the embedding process is to take an image \(I_0\) and to output a visually similar image \(I_w\) carrying the mark or the message.
To do so, we use Stochastic gradient descent over image pixels (like in an adversarial attack) and minimize a loss function that is discribed in more details below.
One SGD iteration of the embedding algorithm is composed of:
- Impose perceptual constraints on the image \(I_w \xleftarrow{\textrm{constraints}} I_w\)
- Sample data-augmentation and apply it to the image \(I_w \xleftarrow{} \textrm{Tr}(I_w,t)\; ; \; t \sim \mathcal T\)
- Compute loss ($\phi$ is the feature extractor) \(\mathcal{L} \gets \lambda \mathcal L_w(\phi (I_w)) + \mathcal L_i(I_w, I_0)\)
- Update the image \(I_w \gets I_w + \eta \times \mathrm{Adam}(\mathcal{L})\)
Hypercone detector
In the 0-bit setup, we are only interested in detecting the presence of the watermark. We use the hypercone detector.
The secret key is a vector \(a\) chosen at random in the feature space \(\|a\|=1\). It defines a dual hypercone of the feature space: \(\mathcal{D} := \left\{ x \in \mathbb{R}^d : \lVert x^T a \rVert > \Vert x \Vert \cos (\theta) \right\}.\)
The Objective function represents how far the feature lies from the hypercone: \(- \mathcal{L}_w(x) = R(x) = (x^\top a)^2 - \|x\|^2 \cos^2\theta.\)
There are theoretical guarantees on the False Positive Rate (FPR): \(\mathrm{FPR} := \mathbb{P}\left(\phi(I)\in \mathcal D \mid \text{"key } a \text{ uniformly distributed"}\right)\nonumber = 1-I_{\cos^2(\theta)} \left(\frac{1}{2}, \frac{d-1}{2} \right).\)
Hyperspace decoding
In the multi-bit setup, we are interested in decoding messages. We modulate the message into the projection of the feature onto a subspace.
The secret key is now a randomly sampled orthogonal family of carriers \(a_1,...., a_k \in \mathbb{R}^d\).
We modulate message \(m = (m_1, ..., m_k) \in \{-1,1\}^k\) into the signs of the projection of the feature \(\phi(I)\) against each of the carriers.
Decoded message:
\(\hat{m} = D(I) = \left[\mathrm{sign}\left(\phi(I)^\top a_1\right), ..., \mathrm{sign}\left(\phi(I)^\top a_k\right)\right].\)
The Objective function is a hinge loss with margin \(\mu\geq 0\) on the projections, to ensure that each projection has the good sign, and with enough margin: \(\mathcal {L}_w(x) = \frac{1}{k} \sum_{i=1}^k \max \left( 0, \mu - (x^\top a_i).m_i \right).\)
Qualitative results
Zero-bit watermarking
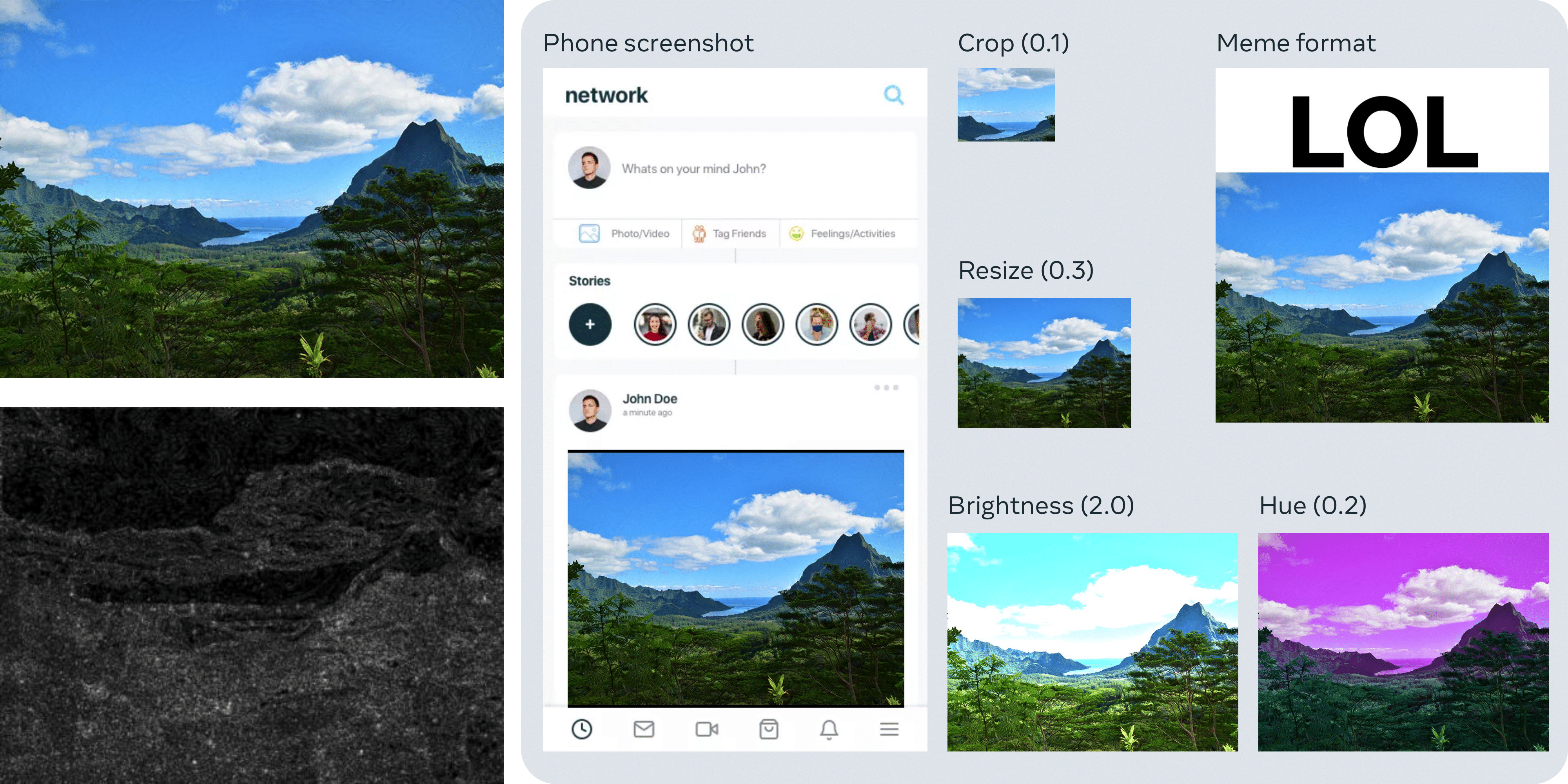
One image (800x600) watermarked at PSNR=40dB and FPR=1e-6, and some detected alterations (the grayscale image is the scaled difference between the original and the watermarked image):
Multi-bit watermarking
We use a 5-bits character encoding to encode and decode one message per image, and show the decoded messages for each image (green means that the character is rightfully decoded). The higher the PSNR, the higher the decoding errors, and the less robust the decoding is to transformations.
One image (1024x768) from the Inria Holidays dataset watermarked at PSNR=40dB and a payload of 30 bits, and decoded messages:

Watermarked images from the Inria Holidays dataset resized to 128x128. The watermark is added with our multi-bit watermarking method with a payload of 30 bits and with different values for the target PSNR: 52dB (top row), 40dB (middle row), 32dB (bottom row).

Quantitative results: Our approach VS state of the art
Zero-bit watermarking
Bellow is the True Positive Rate (TPR) on 118 CLIC images, at PSNR>42 and FPR=1e-6. We can see a noticeable improvement w.r.t. Vukotic’s method.
| Transformation | Id. | Rot. (25) | Crop (0.5) | Crop (0.1) | Resize (0.7) | Blur (2.0) | JPEG (50) | Bright. (2.0) | Contr. (2.0) | Hue (0.25) | Meme | Screenshot |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ours | 1.00 | 1.00 | 1.00 | 0.98 | 1.00 | 1.00 | 0.97 | 0.96 | 1.00 | 1.00 | 1.00 | 0.97 |
| Vukotic (☆) | 1.0 | ≈ 0.3 | ≈ 0.1 | ≈ 0.0 | - | - | ≈ 1.0 | - | - | - | - | - |
| Vukotic (☆☆) | 1.00 | 0.27 | 1.00 | 0.02 | 1.00 | 0.25 | 0.96 | 0.99 | 1.00 | 1.00 | 0.98 | 0.86 |
☆ best results from the paper of Vukotic, ☆☆ our implementation of the same paper.
Multi-bit watermarking
Bellow is the Bit Error Rate (BER) on 1k COCO images resized to 128x128, at PSNR>33, and with a payload of 30 bits. Results are comparable to HiDDeN and Distortion agnostic papers, better for JPEG (never seen at train nor at mark time).
| Transformation | Identity | JPEG (50) | Blur (1.0) | Crop (0.1) | Resize (0.7) | Hue (0.2) |
|---|---|---|---|---|---|---|
| Ours | 0.00 | 0.15 | 0.01 | 0.45 | 0.16 | 0.05 |
| HiDDeN | 0.00 | 0.23 | 0.01 | 0.00 | 0.15 | 0.29 |
| Dist. Agnostic | 0.00 | 0.18 | 0.07 | 0.02 | 0.12 | 0.06 |