TL;DR (Summary)
Recent progress in image generation has made it easy to create and manipulate images in a realistic manner with models like DALL·E~2 and Stable Diffusion. It raises concerns about responsible deployment of these models.
Stable Signature is a watermarking technique that modifies the generative model such that all images it produces hide an invisible signature. These signatures can be used to detect and track the origin of images generated by latent diffusion models.
How does it work?
Image generation with Latent Diffusion Models
Latent Diffusion Models (LDMs) are generative models that produce images by using diffusion processes in the latent space of a variational auto-encoder (like VQ-GAN). The diffusion process is guided by a text prompt, which is used to control the generation of latents. The images are generated by decoding the latents at the end of the diffusion process, with the help of the VAE’s decoder \(D\).

Stable Signature overview
By fine-tuning the decoder of the VAE, we can slightly modify all generated images, such that they hide an invisible signature. In our case, Alice fine-tunes the decoder to produce images that hide a 48-bits binary signature. As an example use-case, her signature can be shared to content sharing platforms. This allows them to know if the content was generated by her model, or identify a specific user who generated content without following her guidelines.

Remarks
Due to potential concerns associated with pre-existing third-party generative models, such as Stable Diffusion or LDMs, we refrain from experimenting with these models and instead use a large diffusion model (2.2B parameters) trained on a proprietary dataset of 330M image-text pairs. However, the variational auto-encoder of our LDM is the same as Stable Diffusion (the one used in LDM with a compression factor of \(f=8\)).
Main results
Images
Examples of images generated by LDMs from text prompts with and without watermarking with Stable Signature. Left: we use the default decoder, without watermark fine-tuning. Middle: we use the decoder with watermark fine-tuning. Right: We show the difference, multiplied by 10 because the distortion is hard to perceive.
Detection & identification
We imagine 2 scenarios where watermarks are used to detect or identify the model that generated an image.
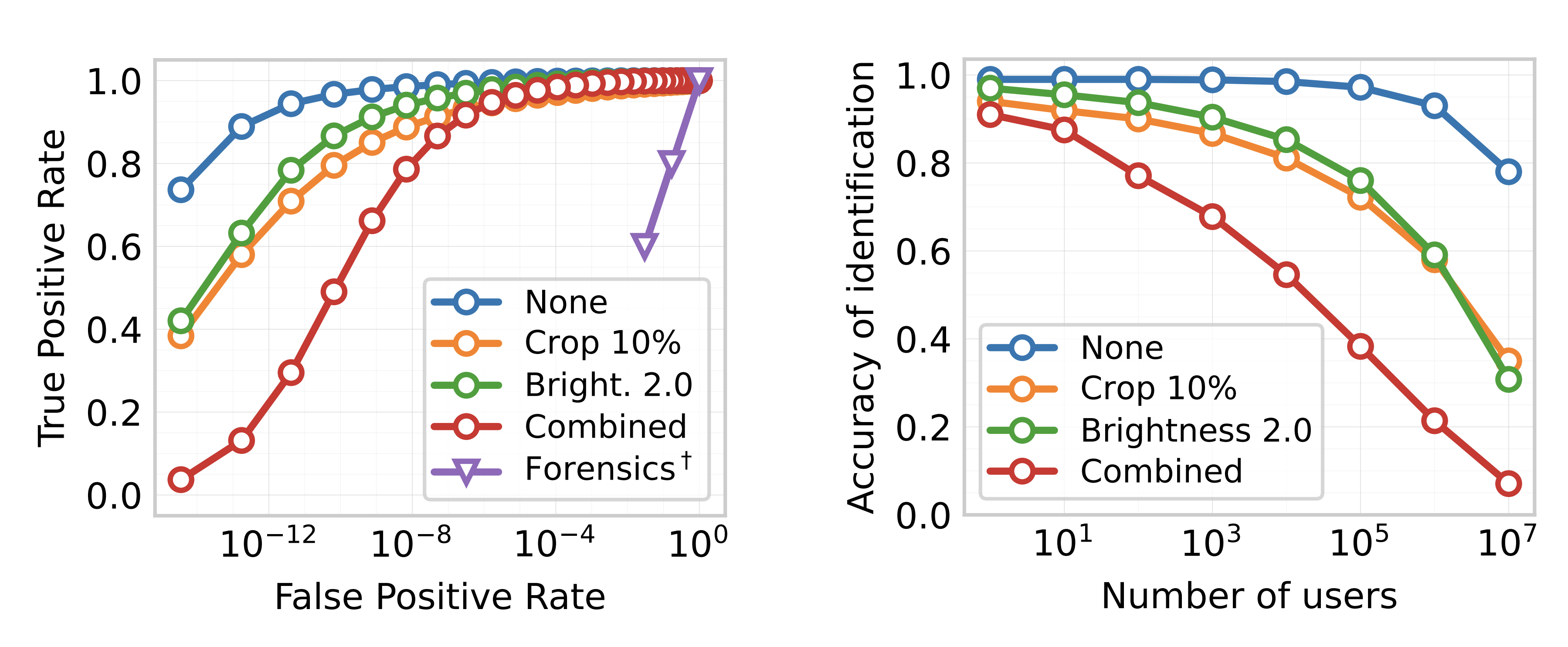
None, Crop, Brightness, Combined refers to the type of transformation applied to the image before detection. (Combined = Crop(0.5) + Brightness(2.0) + JPEG(80))
Detection
In this first scenario, Alice watermarks the decoder with a single signature \(m\), such that all generated images contain this signature. Our goal is to detect if an image \(x\) was generated by a model that uses the signature \(m\), while keeping the false positive rate (FPR) as low as possible, i.e. flag a natural image as least as possible. This is helpful for content sharing platforms, to know if an image was generated by the model.
Our experiments show that:
- Stable Signature detects \(99\%\) of generated images, while only 1 vanilla image out of \(10^9\) is flagged;
- it detects \(84\%\) of generated images for a crop that keeps \(10\%\) of the image (at the same \(\textrm{FPR}=10^{-9}\));
- it detects \(65\%\) for a transformation that combines a crop, a color shift, and a JPEG compression.
Results of state-of-the-art passive methods (applied on resized and compressed images) have orders of magnitudes larger FPR than Stable Signature, which actively marks the content.
Identification
In this second scenario, Alice watermarks the decoder with a different signature \(m\) for each model she gives to Bobs. Given an image, the goal is to find if any of the \(N\) Bobs created it (detection) and if so, which one (identification). There are 3 types of error: false positive: flag a vanilla image; false negative: miss a generated image; false accusation: flag a generated image but identify the wrong user. Alice can trace any misuse of her model: generated images violating her policy (gore content, deepfakes) are linked back to the specific Bob by comparing the extracted message to Bobs’ signatures.
Our experiments show that:
- Stable Signature correctly identifies the user among \(10^5\) in \(98\%\) of generated images when they are not modified;
- it identifies \(40\%\) of generated images for a transformation that combines a crop, a color shift, and a JPEG compression (may still be dissuasive: if a user generates 3 images, he will be identified \(80\%\) of the time);
This is done while keeping an FPR at \(10^{-6}\) (only 1 vanilla image out of \(10^6\) is flagged), and with a false accusation rate of zero, meaning that we never identify the wrong user.
We observe that the identification accuracy decreases when \(N\) increases. In a nutshell, by distributing more models, Alice trades some accuracy of detection against the ability to identify users.
Method details
Watermark pre-training
We jointly train 2 simple convolutional neural networks, in the same way as HiDDeN. The first one (the watermark encoder \(W_E\)) takes as input an image \(x\) and a random \(m\) which is a \(k\)-bit binary message (\(k=48\) in our case). It outputs a new watermark image \(x'\). \(x'\) is then subject to image augmentations such as crops, flips, or JPEG compression. The second one, i.e. the watermark extractor \(W\), takes as input the augmented \(x'\) and outputs the message \(m'\). The goal is to train \(E, W\) such that \(m' = m\).
At the end of this training we discard \(W_E\) that does not serve our purpose and only keep \(W\).
Fine-tuning the LDM decoder
Then, we fine-tune the decoder \(D\) of the VAE into \(D_m\) to produce images that conceal a fixed signature \(m\) (note that all networks are fixed unless \(D_m\)). This is inspired by the training procedure of LDM. During a loop of the fine-tuning, a batch \(x\) of training images is encoded, then decoded by \(D\), resulting in images \(x'\). The loss to be minimized is then computed as a weighted sum of the message loss \(L_{m}\), which aims at minimizing the distance between the extracted message \(m'\) and the target message \(m\), and the perceptual image loss \(L_{i}\), which aims at generating images close to the original ones.
This optimization can be performed very quickly. In our experiments, we use batch size 4 and \(100\) iterations are enough to reach a very high quality (around 1 minute).
Statistical tests
Once we retrieve the signature \(m'\) from an image \(x'\), we use statistical tests to determine if the image was generated by one of our model. This gives theorethical values for the false positive rates, i.e. the probability of falsely detecting an image as generated by one of our models.
We will use the number of matching bits \(M(m,m')\) between the extracted message \(m'\) and the signature \(m\) of the model to measure the distance between the two messages.
Detection
We assume Alice has embedded a \(k\)-bits signature \(m\) in the decoder \(D_m\).
We test the statistical hypothesis \(H_1\): ”\(x\) was generated by Alice’s model” against the null hypothesis \(H_0\): \(x\) was not generated by Alice’s model. We compute the number of matching bits \(M\) between \(m'\): the message extracted from \(x\), and the signature \(m\). We decide to flag the image \(x\) as generated by Alice’s model if \(M\) is greater than a threshold \(\tau\).
The FPR of the detection is then given by:
\[\begin{aligned} \text{FPR}(\tau) &= \mathbb{P}\left(M(m, m') > \tau | H_0\right) \\ &= \frac{1}{2^k}\sum_{i=\tau+1}^k \binom{k}{i}. \end{aligned}\]Identification
We assume Alice has embedded \(N\) different signatures \(m^{(1)}, \ldots, m^{(N)}\) in the decoders \(D_{m^{(1)}}, \ldots, D_{m^{(N)}}\), drawn randomly from \(\{0,1\}^k\) (one for every Bob). There are now \(N\) detection hypotheses to test. If the \(N\) hypotheses are rejected, we can conclude that the image was not generated by any of the models.
The FPR of the identification is then given by:
\[\begin{aligned} \text{FPR}(\tau,N) &= 1-(1-\text{FPR}(\tau))^N \\ &\approx N.\text{FPR}(\tau). \end{aligned}\]Slides (FR)